3.5 Correlated Error Terms

In model (1.1) , we assume the error terms are uncorrelated.

In the normal errors model (2.1) , we assume the error terms are independent.

We noted in Section 2.1.1 that the normal error model assumed that any pair of error terms $\varepsilon_i$ and $\varepsilon_j$ are jointly normal. Since they are jointly normal, then uncorrelated implied independence.

In general, uncorrelated does not imply independence. It only implies it in the normal errors model due to the joint normal distribution.

Since we are assuming the normal errors model, we want to check to see the uncorrelated errors assumption. If there is no correlation between the residuals, then we can assume independence.

The usual cause of correlation in the residuals is data taken in some type of sequence such as time or space. When the error terms are correlated over time or some other sequence, we say they are serially correlated or autocorrelated.

When the data are taken in some sequence, a sequence plot of the residuals may show a pattern indicating autocorrelation. In a sequence plot, the residuals are plotted against the observation index $i$. If there is no autocorrelation, then the residuals should be "randomly" spread about zero. If there is a pattern, then there is evidence of autocorrelation.

Sometime a residual sequence plot may not show an obvious pattern but autocorrelation may still exist.

Another plot that helps examine correlation that may not be visible in the sequence plot is the autocorrelation function plot (ACF).

In the ACF plot, correlations are calculated between residuals some $k$ index away. That is, \begin{align*} r_{k} & =\widehat{Cor}\left[e_{i},e_{i+k}\right]\\ & =\frac{\sum_{i=1}^{n-k}\left(e_{i}-\bar{e}\right)\left(e_{i+k}-\bar{e}\right)}{\sum_{i=1}^{n}\left(e_{i}-\bar{e}\right)^{2}}\qquad\qquad(3.4) \end{align*} In an ACF plot, $r_k$ is plotted for varying values of $k$. If the value of $r_k$ is larger in magnitude than some threshold shown on the plot (usually a 95% confidence interval), then we consider this evidence of autocorrelation.

In addition to examining serial plots and ACF plots, tests can be conducted for significant autocorrelation. In each of these tests, the null hypothesis is there is no autocorrelation.

The Durbin-Watson test is for autocorrelation at $k=1$ in (3.4) . That is, it tests for correlation one index (one time point) away.

The Durbin-Watson test can be conducted in R with the dwtest function in the lmtest package.

The Ljung-Box test differs from the Durbin-Watson test in that it tests for overall correlation over all lags up to $k$ in (3.4) . For example, if $k=4$ then the Ljung-Box test is for significant autocorrelation over all lags up to $k=4$.

The Ljung-Box test can be conducted in R with the Box.test function with the argument type=("Ljung"). This function is in base R.

The Breusch-Godfrey test is similar to the Ljung-Box test in that it tests for overall correlation over all lags up to $k$. The difference between the two test is not of concern in the regression models we will examine in this course. When using time series models, then the Breusch-Godfrey test is preferred over the Ljung-Box test due to asymptotic justification.

The Breusch-Godfrey test can be conducted in R with the bgtest function in the lmtest package.

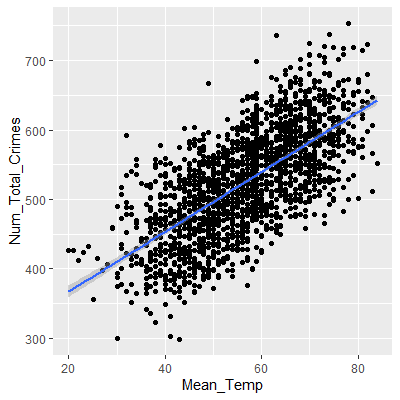
Let's look at data collected on the mean temperature for each day in Portland, OR, and the number of non-violent crimes reported that day. The crime data was part of a public database gathered from www.portlandoregon.gov. The data are presented in order by day. The variable X in the dataset is the day index number.

library(tidyverse)
library(lmtest)
library(forecast)

dat = read.table("http://www.jpstats.org/Regression/data/PortlandWeatherCrime.csv", header=T, sep=",")

ggplot(dat, aes(x=Mean_Temp, y=Num_Total_Crimes))+
  geom_point()+
  geom_smooth(method="lm")


fit = lm(Num_Total_Crimes~Mean_Temp, data=dat)
fit %>% summary
Call:
lm(formula = Num_Total_Crimes ~ Mean_Temp, data = dat)

Residuals:
     Min       1Q   Median       3Q      Max 
-168.198  -41.055    0.149   40.455  183.680 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 281.0344     6.4456   43.60   <2e-16 ***
Mean_Temp     4.3061     0.1116   38.59   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 55.69 on 1765 degrees of freedom
Multiple R-squared:  0.4576,	Adjusted R-squared:  0.4573 
F-statistic:  1489 on 1 and 1765 DF,  p-value: < 2.2e-16

dat$res = fit %>% resid()

ggplot(dat, aes(x=X, y=res))+
  geom_point()

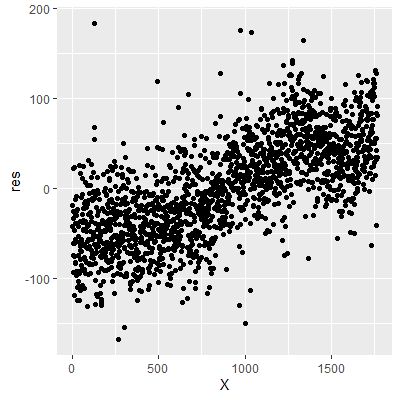
We can see that the residuals have a pattern where the values at the lower levels of the index tend to be below zero whereas the values at the higher levels of the index tend to be above zero. This is evidence of autocorrelation in the residuals.

ggAcf(dat$res)

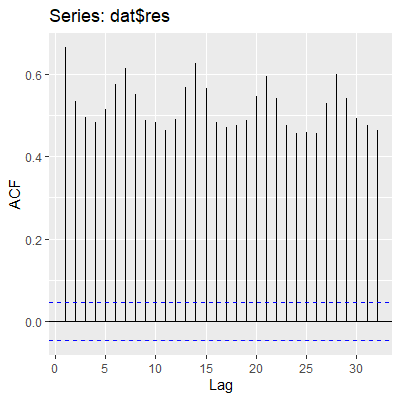
The values of the ACF at all lags are beyond the blue guideline for significant autocorreleation.

Note that in the Ljung-Box test and the Breusch-Godfrey test below, we tested up to lag 7. We chose this lag since the data was taken over time and it would make sense for values at seven days apart to be similar. That is, we expect the number of crimes on Mondays to be similar, the number of crimes on Tuesdays to be similar, etc.

dwtest(fit)

	Durbin-Watson test

data:  fit
DW = 0.66764, p-value < 2.2e-16
alternative hypothesis: true autocorrelation is greater than 0

Box.test(dat$res, lag=7,type="Ljung")

	Box-Ljung test

data:  dat$res
X-squared = 3865, df = 7, p-value < 2.2e-16

bgtest(fit, order=7)

	Breusch-Godfrey test for serial correlation of order up to 7

data:  fit
LM test = 977.84, df = 7, p-value < 2.2e-16



                            

When the assumption of independence is violated, then a difference in the $Y$ values could help remove the autocorrelation. This difference is $$ Y^{\prime} = Y_i - Y_{i-k} $$ where $k$ is some max lag where autocorrelation is significant. This difference $Y^{\prime}$ is then regressed on $X$. This difference may not help, in which case a time series model would be necessary.