Fill in Blanks
Home
1.1 Bivariate Relationships 1.2 Probabilistic Models 1.3 Estimation of the Line 1.4 Properties of the Least Squares Estimators 1.5 Estimation of the Variance
2.1 The Normal Errors Model 2.2 Inferences for the Slope 2.3 Inferences for the Intercept 2.4 Correlation and Coefficient of Determination 2.5 Estimating the Mean Response 2.6 Predicting the Response
3.1 Residual Diagnostics 3.2 The Linearity Assumption 3.3 Homogeneity of Variance 3.4 Checking for Outliers 3.5 Correlated Error Terms 3.6 Normality of the Residuals
4.1 More Than One Predictor Variable 4.2 Estimating the Multiple Regression Model 4.3 A Primer on Matrices 4.4 The Regression Model in Matrix Terms 4.5 Least Squares and Inferences Using Matrices 4.6 ANOVA and Adjusted Coefficient of Determination 4.7 Estimation and Prediction of the Response
5.1 Multicollinearity and Its Effects 5.2 Adding a Predictor Variable 5.3 Outliers and Influential Cases 5.4 Residual Diagnostics 5.5 Remedial Measures
6.1 Indicator Variables 6.2 Interaction Between Predictors
7.1 Model Selection Criteria 7.2 Best Subsets Procedure 7.3 Stepwise Regression Procedures 7.4 Lasso 7.5 Model Validation
8.1 Logistic Regression 8.2 Multinomial Logistic Regression 8.3 Ordinal Regression 8.4 Poisson Regression

1.1 Bivariate Relationships

"Relationships? We don't need no stinking relationships!" -Michael Scott

1.1.1 Examining Data

When examining one set of data, we usually want to describe it using some basic statistics such as the mean $$\bar{Y} = \frac{1}{n}\sum_{i=1}^n Y_i $$ and the standard deviation $$ s = \sqrt{\frac{1}{n-1}\sum_{i=1}^n \left(Y_i-\bar{Y}\right)^2} $$

Recall that $\bar{Y}$ is a measure of central tendency and $s$ is a measure of variability

That is, we have a measure of where the "center" of the data tends to locate and a measure of how "spread out" is the data.

We also will want to visualize the data with a plot such as a scatterplot or a histogram.

Handspan data - Summary

Suppose we have a sample of size $n=834$ of college students and we record their right handspan (in cm).

Since there is only one variable, the scatterplot will only show the data at it relates to one axis. Here, let's plot on the x-axis.

It is difficult to visualize the data in this one-dimensional scatterplot since some of the points overlap each other.

A histogram will help us visualize the data better.

So for this data, we have a mean of

which is represented by the red line in Figure 1.1.1, and a standard deviation of

Figure 1.1.1: Handspan data

Handspan and height

Suppose we have some other information about each student. For example, suppose we also knew each student's height

It would make sense that students who are taller will tend to have larger handspans.

So let's include height with handspan. We will make the handspan be the $Y$ variable and plot it on the $Y$ (vertical) axis:

We will now include the heights on the $X$ axis.

Figure 1.1.2: Handspan and height scatterplot

From the scatterplot with both handspan and height, we can see a general pattern. That is, those with larger heights tend to have handspans that are larger.

This does not mean that a person shorter than another will necessarily have a smaller handspan. But, in general, those that are taller tend to have larger handspans.

In terms of central tendency, we can now describe the mean handspan for different values of height. When we only had the handspan variable, we had measure of central tendency that was one value ($\bar{Y}=20.06$). Now that we have the added variable of height, the central tendency can change for different values of height.

For example, there were 68 students with a height of 65 inches. The average handspan for these students with a height of 65 inches is $\bar{Y}=19.67$.

Likewise, the average handspan for the 63 students with a height of 70 inches is $\bar{Y}=21.08$.

1.1.2 Types of Bivariate Relationships

In Figure 1.1.2, the scatterplot shows the general relationship between handspan ($Y$) and height ($X$). When we have two variables, we call the relationship a bivariate relationship. When we only had one variable to examine (handspan), we were interested in a univariate analysis. When we include the second variable, we now are interested in a bivariate analysis

Types of relationships

We see in Figure 1.1.2, that the relationship between handspan and height is linear. That is, handspan tends to increase, on average, in a linear fashion when height changes.

The relationship between $X$ and $Y$ may be something other than linear. It could be that the $Y$ changes in an exponential, sinusoidal, or some other fashion. Figure 1.1.3 below shows just a few of the different types of relationships that could exist between $X$ and $Y$.

Figure 1.1.3: Types of Bivariate Relationships

Types of Bivariate Relationships

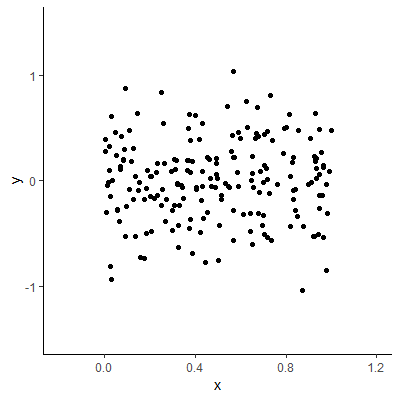
We could also have no clear relationship between $X$ and $Y$. In Figure 1.1.4 below, $Y$ does not appear to be changing in any clear pattern as $X$ changes.

Figure 1.1.4: No Clear Bivariate Relationship

No clear relationship

In regression analysis, we will theorize a model to describe the relationship between $X$ and $Y$.

The type of relationship between $X$ and $Y$ will help us choose an appropriate model.

Because of this, our first step in a regression analysis for two variables is to examine the scatterplot of the variables.