Fill in Blanks
Home
1.1 Bivariate Relationships
1.2 Probabilistic Models
1.3 Estimation of the Line
1.4 Properties of the Least Squares Estimators
1.5 Estimation of the Variance
2.1 The Normal Errors Model
2.2 Inferences for the Slope
2.3 Inferences for the Intercept
2.4 Correlation and Coefficient of Determination
2.5 Estimating the Mean Response
2.6 Predicting the Response
3.1 Residual Diagnostics
3.2 The Linearity Assumption
3.3 Homogeneity of Variance
3.4 Checking for Outliers
3.5 Correlated Error Terms
3.6 Normality of the Residuals
4.1 More Than One Predictor Variable
4.2 Estimating the Multiple Regression Model
4.3 A Primer on Matrices
4.4 The Regression Model in Matrix Terms
4.5 Least Squares and Inferences Using Matrices
4.6 ANOVA and Adjusted Coefficient of Determination
4.7 Estimation and Prediction of the Response
5.1 Multicollinearity and Its Effects
5.2 Adding a Predictor Variable
5.3 Outliers and Influential Cases
5.4 Residual Diagnostics
5.5 Remedial Measures
2.4 Correlation and Coefficient of Determination
Now that we can fit the model to the data, we want to assess how "good" of a fit we have.
We will present two measures that will quantify how well the model fits the data.
We will present two measures that will quantify how well the model fits the data.
For the data $(X_i,Y_i)$, $i=1,\ldots,n$, we want a measure of how well a linear model explains a linear relationship between $X$ and $Y$.
We start by defining $$ SS_{XX} = \sum\left(X_i-\bar{X}\right)^2\qquad\qquad\qquad(2.11) $$ and $$ SS_{YY} = \sum\left(Y_i-\bar{Y}\right)^2\qquad\qquad\qquad(2.12) $$ $SS_{XX}$ and $SS_{YY}$ are measures ofvariability of $X$ and $Y$, respectively. That is, they indicate how $X$ and $Y$ vary about their mean, individually.
Now, we define $$ SS_{XY}=\sum\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)\qquad\qquad\qquad(2.13) $$ $SS_{XY}$ is a measure of how $X$ and $Y$ varies together.
We start by defining $$ SS_{XX} = \sum\left(X_i-\bar{X}\right)^2\qquad\qquad\qquad(2.11) $$ and $$ SS_{YY} = \sum\left(Y_i-\bar{Y}\right)^2\qquad\qquad\qquad(2.12) $$ $SS_{XX}$ and $SS_{YY}$ are measures of
Now, we define $$ SS_{XY}=\sum\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)\qquad\qquad\qquad(2.13) $$ $SS_{XY}$ is a measure of how $X$ and $Y$ varies together.
For example, consider the data from Figure 1.3.1
. Let's find $SS_{XX}$, $SS_{YY}$, and $SS_{XY}$ in R.
In the output ofdat1 , dev_x^2 represents $(X_i-\bar{X})^2$ and dev_y^2 represents $(Y_i-\bar{Y})^2$ for each observation.
dev_xy represents $(X_i-\bar{X})(Y_i-\bar{Y})$ for each observation. Note that each value is negative. This is because as $X$ is below $\bar{X}$, $Y$ is above $\bar{Y}$. Likewise, as $X$ is above $\bar{X}$, $Y$ is below $\bar{Y}$. In the ggplot above, the two red lines represent $\bar{X}$ (the vertical red line) and $\bar{Y}$ (the horizontal red line). You can see how the observations are below or above these lines.
We can find the values of $SS_{XX}$, $SS_{YY}$, and $SS_{XY}$ by
library(tidyverse)
x = c(1,2 ,2.75, 4, 6, 7, 8, 10)
y = c(2, 1.4, 1.6, 1.25, 1, 0.5, 0.5, 0.4)
dat = tibble(x,y)
ybar = mean(y)
xbar = mean(x)
ggplot(dat, aes(x=x,y=y))+
geom_point()+
xlim(0,10)+
ylim(0,2)+
geom_hline(yintercept = ybar,col="red")+
geom_vline(xintercept = xbar, col="red")
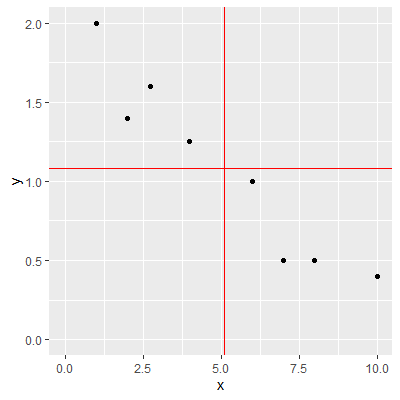
dev_x = x-xbar
dev_y = y-ybar
dev_xy = dev_x*dev_y
dat1 = tibble(x,y,dev_x^2,dev_y^2,dev_xy)
dat1
x y `dev_x^2` `dev_y^2` dev_xy
1 1 2 16.8 0.844 -3.76
2 2 1.4 9.57 0.102 -0.986
3 2.75 1.6 5.49 0.269 -1.22
4 4 1.25 1.20 0.0285 -0.185
5 6 1 0.821 0.00660 -0.0736
6 7 0.5 3.63 0.338 -1.11
7 8 0.5 8.45 0.338 -1.69
8 10 0.4 24.1 0.464 -3.34
In the output of
We can find the values of $SS_{XX}$, $SS_{YY}$, and $SS_{XY}$ by
#SS_XX
dev_x^2 %>% sum()
[1] 69.99219
[1] 2.389687
[1] -12.36094
For another example, consider the trees dataset from Example 2.2.1. Again, we plot the data with red lines representing $\bar{X}$ and $\bar{Y}$.
In this example, most of the observations have $(X-\bar{X})(Y-\bar{Y})$ that are positive. This is because these observations have values of $X$ that are below $\bar{X}$ and values of $Y$ that are below $\bar{Y}$, or values of $X$ that are above $\bar{X}$ and values of $Y$ that are above $\bar{Y}$.
There are four observations that have a negative value of $(X-\bar{X})(Y-\bar{Y})$. Although they are negative, the value of $SS_{XY}$ is positive due to all the observations with positive values of $(X-\bar{X})(Y-\bar{Y})$. Therefore, we say if $SS_{XY}$ ispositive , then $Y$ tends to increase as $X$ increases. Likewise, if $SS_{XY}$ is negative , then $Y$ tends to decrease as $X$ increases.
If $SS_{XY}$ is zero (or close to zero), then we say $Y$ does not tend to change as $X$ increases.
library(datasets)
library(tidyverse)
xbar = mean(trees$Girth)
ybar = mean(trees$Volume)
ggplot(data=trees, aes(x=Girth, y=Volume))+
geom_point()+
geom_hline(yintercept = ybar,col="red")+
geom_vline(xintercept = xbar, col="red")
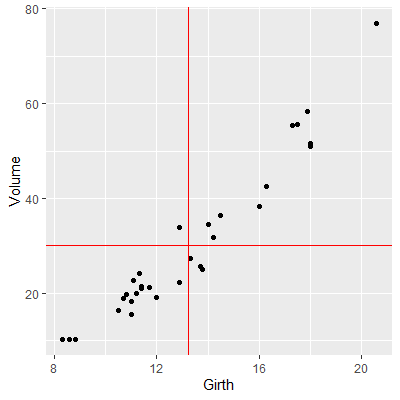
x = trees$Girth
y = trees$Volume
dev_x = x-xbar
dev_y = y-ybar
dev_xy = dev_x*dev_y
dat1 = tibble(x,y,dev_x^2,dev_y^2,dev_xy)
dat1 %>% print(n=31)
x y `dev_x^2` `dev_y^2` dev_xy
1 8.3 10.3 24.5 395. 98.3
2 8.6 10.3 21.6 395. 92.4
3 8.8 10.2 19.8 399. 88.8
4 10.5 16.4 7.55 190. 37.8
5 10.7 18.8 6.49 129. 29.0
6 10.8 19.7 5.99 110. 25.6
7 11 15.6 5.06 212. 32.8
8 11 18.2 5.06 143. 26.9
9 11.1 22.6 4.62 57.3 16.3
10 11.2 19.9 4.20 105. 21.0
11 11.3 24.2 3.80 35.7 11.6
12 11.4 21 3.42 84.1 17.0
13 11.4 21.4 3.42 76.9 16.2
14 11.7 21.3 2.40 78.7 13.7
15 12 19.1 1.56 123. 13.8
16 12.9 22.2 0.121 63.5 2.78
17 12.9 33.8 0.121 13.2 -1.26
18 13.3 27.4 0.00266 7.68 -0.143
19 13.7 25.7 0.204 20.0 -2.02
20 13.8 24.9 0.304 27.8 -2.91
21 14 34.5 0.565 18.7 3.25
22 14.2 31.7 0.906 2.34 1.46
23 14.5 36.3 1.57 37.6 7.67
24 16 38.3 7.57 66.1 22.4
25 16.3 42.6 9.31 154. 37.9
26 17.3 55.4 16.4 637. 102.
27 17.5 55.7 18.1 652. 109.
28 17.9 58.3 21.6 791. 131.
29 18 51.5 22.6 455. 101.
30 18 51 22.6 434. 99.0
31 20.6 77 54.0 2193. 344.
[1] 295.4374
[1] 8106.084
[1] 1496.644
In this example, most of the observations have $(X-\bar{X})(Y-\bar{Y})$ that are positive. This is because these observations have values of $X$ that are below $\bar{X}$ and values of $Y$ that are below $\bar{Y}$, or values of $X$ that are above $\bar{X}$ and values of $Y$ that are above $\bar{Y}$.
There are four observations that have a negative value of $(X-\bar{X})(Y-\bar{Y})$. Although they are negative, the value of $SS_{XY}$ is positive due to all the observations with positive values of $(X-\bar{X})(Y-\bar{Y})$. Therefore, we say if $SS_{XY}$ is
If $SS_{XY}$ is zero (or close to zero), then we say $Y$ does not tend to change as $X$ increases.
We first note that $SS_{XY}$ cannot be greater in absolute value than the quantity
$$
\sqrt{SS_{XX}SS_{YY}}
$$
We will not prove this here, but it is a direct application of the Cauchy-Schwarz inequality.
We define thelinear correlation coefficient as
$$
r=\frac{SS_{XY}}{\sqrt{SS_{XX}SS_{YY}}}\qquad\qquad\qquad(2.13)
$$.
$r$ is also called thePearson correlation coefficient.
We note that $$ -1\le r \le 1 $$
If $r=0$, then there is no linear relationship between $X$ and $Y$.
If $r$ is positive, then the slope of the linear relationship is positive. If $r$ is negative, then the slope of the linear relationship is negative.
The closer $r$ is to one in absolute value, the stronger the linear relationship is between $X$ and $Y$.
We define the
$r$ is also called the
We note that $$ -1\le r \le 1 $$
If $r=0$, then there is no linear relationship between $X$ and $Y$.
If $r$ is positive, then the slope of the linear relationship is positive. If $r$ is negative, then the slope of the linear relationship is negative.
The closer $r$ is to one in absolute value, the stronger the linear relationship is between $X$ and $Y$.
The best way to grasp correlation is to see examples. In Figure 2.4.1, a scatterplot of a 200 observations is shown with a least squares line. The value of $r$ for this sample is shown below. The plot will update with a new sample every ten seconds.
Figure 2.4.1: Examples of Correlation
The correlation $r$ is for the observed data which is usually from a sample. Thus, $r$ is the sample correlation coefficient.
We could make a hypothesis about the correlation of thepopulation based on the sample. We will denote the population correlation with $\rho$. The hypothesis we will want to test is
$$
H_0:\rho = 0\\
H_1:\rho \ne 0
$$
We could make a hypothesis about the correlation of the
Recall from Section 2.2.4 that (2.6)
If we test \begin{align*} H_{0}: & \beta_{1}=0\\ H_{a}: & \beta_{1}\ne0 \end{align*} then this is equivalent to testing \begin{align*} H_{0}: & \rho=0\\ H_{a}: & \rho\ne0 \end{align*} since both hypotheses test to see of there is no linear relationship between $X$ and $Y$.
Now note, using (1.4)
Also, $SSE$ from (1.16)
If $H_0$ is true, then $t$ will have a Student's $t$-distribution with $n-2$ degrees of freedom.
\begin{align*}
t= & \frac{b_{1}-\beta_{1}^{0}}{\sqrt{\frac{s^{2}}{\sum\left(X_{i}-\overline{X}\right)^{2}}}}\qquad\qquad\qquad(2.6)
\end{align*}
can be used to test a hypothesis
for the slope.
If we test \begin{align*} H_{0}: & \beta_{1}=0\\ H_{a}: & \beta_{1}\ne0 \end{align*} then this is equivalent to testing \begin{align*} H_{0}: & \rho=0\\ H_{a}: & \rho\ne0 \end{align*} since both hypotheses test to see of there is no linear relationship between $X$ and $Y$.
Now note, using (1.4)
\begin{align*}
b_{0} & =\bar{Y}-b_{1}\bar{X}\\
b_{1} & =\frac{\sum \left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sum \left(X_{i}-\bar{X}\right)^{2}}\qquad\qquad\qquad(1.4)
\end{align*}
, that $b_{1}$ can be rewritten as
\begin{align*}
b_{1} & =\frac{\sum\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sum\left(X_{i}-\bar{X}\right)^{2}}\\
& =\frac{SS_{XY}}{SS_{XX}}\\
& =\frac{rSS_{XY}}{rSS_{XX}}\\
& =\frac{rSS_{XY}}{\frac{SS_{XY}}{\sqrt{SS_{xx}SS_{YY}}}SS_{XX}}\\
& =\frac{r\sqrt{SS_{XX}SS_{YY}}}{SS_{XX}}\\
& =r\frac{\sqrt{\frac{SS_{XX}}{n-1}\frac{SS_{YY}}{n-1}}}{\frac{SS_{XX}}{n-1}}\\
& =r\frac{s_{X}s_{Y}}{s_{X}^{2}}\\
& =r\frac{s_{y}}{s_{X}}\qquad\qquad\qquad(2.14)
\end{align*}
where $s_{Y}$ and $s_{X}$ are the sample standard deviation of $Y$
and $X$, respectively.
Also, $SSE$ from (1.16)
$$
SSE = \sum \left(Y_i - \hat{Y}_i\right)^2\qquad\qquad\qquad(1.16)
$$
can be rewritten as
\begin{align*}
SSE & =\sum\left(Y_{i}-\hat{Y}_{i}\right)^{2}\\
& =\sum\left(Y_{i}-\underbrace{b_{0}}_{(1.4)}-b_{1}X_{i}\right)^{2}\\
& =\sum\left(Y_{i}-\overline{Y}+b_{1}\overline{X}-b_{1}X_{i}\right)^{2}\\
& =\sum\left(\left(Y_{i}-\overline{Y}\right)-b_{1}\left(X_{i}-\overline{X}\right)\right)^{2}\\
& =\sum\left(\left(Y_{i}-\overline{Y}\right)^{2}-2b_{1}\left(X_{i}-\overline{X}\right)\left(Y_{i}-\overline{Y}\right)+b_{1}^{2}\left(X_{i}-\overline{X}\right)^{2}\right)\\
& =SS_{YY}-2\underbrace{b_{1}}_{(1.4)}SS_{XY}+b_{1}^{2}SS_{XX}\\
& =SS_{YY}-2\left(\frac{SS_{XY}}{SS_{XX}}\right)SS_{XY}+\left(\frac{SS_{XY}}{SS_{XX}}\right)^{2}SS_{XX}\\
& =SS_{YY}-\left(\frac{SS_{XY}}{SS_{XX}}\right)SS_{XY}\\
& =SS_{YY}-\underbrace{b_{1}}_{(2.14)}SS_{XY}\\
& =SS_{YY}-r\left(\frac{\sqrt{SS_{YY}}}{\sqrt{SS_{XX}}}\right)SS_{XY}\\
& =SS_{YY}\left(1-r\frac{SS_{XY}}{\sqrt{SS_{XX}}\sqrt{SS_{YY}}}\right)\\
& =SS_{YY}\left(1-r^{2}\right)\qquad\qquad\qquad\qquad(2.15)
\end{align*}
Now, using (2.14) and (2.15), we write the test statistic as
\begin{align*}
t & =\frac{b_{1}}{\sqrt{\frac{s^{2}}{\sum\left(X_{i}-\bar{X}\right)^{2}}}}\\
& =\frac{r\frac{s_{y}}{s_{X}}}{\sqrt{\frac{SSE}{\left(n-2\right)SS_{XX}}}}\\
& =\frac{r\frac{s_{y}}{s_{X}}}{\sqrt{\frac{SS_{YY}\left(1-r^{2}\right)}{\left(n-2\right)SS_{XX}}}}\\
& =\frac{r\frac{s_{y}}{s_{X}}}{\sqrt{\frac{\left(1-r^{2}\right)s_{Y}^{2}}{\left(n-2\right)s_{X}^{2}}}}\\
& =\frac{r\frac{s_{y}}{s_{X}}\sqrt{\left(n-2\right)}}{\frac{s_{y}}{s_{X}}\sqrt{1-r^{2}}}\\
& =\frac{r\sqrt{\left(n-2\right)}}{\sqrt{1-r^{2}}}\qquad\qquad\qquad(2.16)
\end{align*}
If $H_0$ is true, then $t$ will have a Student's $t$-distribution with $n-2$ degrees of freedom.
The second measure of how well the model fits the data involves measuring the amount of variability in $Y$ that is explained by the model using $X$.
We start by examining the variability of the variable we want to learn about. We want to learn about the response variable $Y$. One way to measure the variability of $Y$ is with
$$
SS_{YY} = \sum\left(Y_i-\bar{Y}\right)^2\qquad\qquad\qquad(2.12)
$$
Note that $SS_{YY}$ does not include the model or $X$. It is just a measure of how $Y$ deviates from its mean $\bar{Y}$.
We also have the variability of the points about theline . We can measure this with the sum of squares error
$$
SSE = \sum \left(Y_i - \hat{Y}_i\right)^2\qquad\qquad\qquad(1.16)
$$
Note that SSE does include $X$. This is because the fitted line $\hat{Y}$ is a function of $X$.
We also have the variability of the points about the
Let's look again at the Handspan and Height data from Section 1.1.
If using $X$ in the model does not help in explaining $Y$, then the regression line will be horizontal. That is, the slope will be zero. In that case, $SS_{YY}$ and SSE will be the same .
If using $X$ in the model helps substantially in explaining $Y$, then the points should be somewhat close to the regression line. Therefore, SSE will be muchsmaller than $SS_{YY}$.
In Figure 2.4.2, the Handspan variable is the response variable $Y$. By itself, we see the data plotted on the vertical axis. $SS_{YY}$ is a measure of how spread out the data are on the vertical axis.
If we include the variable Height as our $X$ and then fit model (2.1)
The blue brace in the plot represents the spread about the regression line which can be measured by SSE.
If we include the variable Height as our $X$ and then fit model (2.1)
\begin{align*}
Y_i=&\beta_0+\beta_1X_i+\varepsilon_i\\
\varepsilon_i\overset{iid}{\sim}& N\left(0,\sigma^2\right)\qquad\qquad\qquad\qquad(2.1)
\end{align*}
, then we can see how spread the data are about the regression line (red in Figure 2.4.2).
The blue brace in the plot represents the spread about the regression line which can be measured by SSE.
Figure 2.4.2: Illustration of $SS_{YY}$ and SSE
If using $X$ in the model helps substantially in explaining $Y$, then the points should be somewhat close to the regression line. Therefore, SSE will be much
We want to explain as much of the variation of $Y$ as possible. So we want to know just how much of that variation is explained by using linear regression model with $X$. We can quantify this variation explained by taking the difference
$$
SSR = SS_{YY}-SSE\qquad\qquad\qquad(2.17)
$$
SSR is called the sum of squares regression .
We calculate theproportion of the variation of $Y$ explained by the regression model using $X$ by calculating
$$
R^2 = \frac{SSR}{SS_{YY}}\qquad\qquad\qquad(2.18)
$$
$R^2$ is called the coefficient of determination .
We calculate the
